サンプル例1、例2の内容

例1、例2は、transition:all 1s linear を指定しています。
【例1】 マウスホバーで A : skewX (30deg)、B : skewY (30deg) を指定した例。

【例2】 マウスホバーで C : skewX (-30deg)、D : skewY (-30deg)を指定した例。
※例1の値をマイナスにした場合

例1へ

サンプル例3、例3bの内容

例3、例3bは、transition:all 1s linear を指定しています。
【例3】 マウスホバーで E : [skew (30deg,20deg)] と、F : [skewX(30deg) skewY(20deg)] の比較です。F の方が横への変形が大きくなっています。
変形の様子が違うのは、matrixに変換した時に、E が matrix(1, 0.36397, 0.57735, 1, 0, 0) で、F が matrix(1.21014, 0.36397, 0.57735, 1, 0, 0) になっているからです。

※ transform関連は複数のプロパティを指定した時は、指定順で変化が違って見える形になりますが、これは各プロパティ値をmatrix値に変換する時の小数誤差や小数点以下の切り上げなどの計算処理によって最終的なmatrix値が違う値になるからだと思われます。
※なので、原森webの Transform ソース作成ツールではプロパティの並び替え機能を追加しています。

【例3b】skewY(20deg) skewX(30deg) の順序で指定した場合との比較です。(※ G は例3の E と同じ指定です )
H : matrix(1, 0.36397, 0.57735, 1.21014, 0, 0)となり、E ( = G ) の skew (30deg,20deg) = matrix(1, 0.36397, 0.57735, 1, 0, 0) とmatrix値が一部違っています。
先にＹ軸に変形しているのでこちらは縦への変形が大きくなっています。

※ skew (30deg,20deg) のようなX軸Y軸を両方指定する記述は非推奨になったようですので、[skewX(…) skewY(…)] か、[skewY(…) skewX(…)]のように指定することになるかと思いますが、指定順で変形する形が異なりますので注意が必要です。

例3へ

サンプル例4の内容

【例4】 skewのyの値を省略した時の比較です。（マウスホバー演出なしです）I : skew (30deg)、J : skewX (30deg)。仕様通り、skew (30deg) = skewX (30deg) となっています。

例4へ

サンプル例5、例5bの内容

【例5】 transition:all 1s linear を指定しています。
rotateと同様に、値が 360deg や 180deg だとどうなるかを実験してみました。
白枠ホバーでそれぞれ同時に変化しますが、180degの場合、1回転しているように見え、360degだと2回転するようにみえます。

【例5b】 transition:all 5s linear を指定しています。
秒数を5sにしてゆっくり変化させてみると、斜めに歪んで線になり、そのまま反対に歪んで最初の形に戻るような変形になっています。
さらに変化中、文字が逆さにならないのが印象的な感じです。
(rotate は回転なので180degで文字が上下左右逆さまになります)

例5へ

サンプル例6の内容

【例6】変形アニメの途中なら、その状態を省略して前後の形からの変化でごまかしたりしてるかと思いますが、無限の長さの直線になる可能性のある、危険な印象の skewX(90deg) と skewY(90deg) で停止する指定を実験してみました。

M に skewX(90deg) を指定して実験し、横につぶれて直線になってブラウザ上では見えない（厚さの概念がないから）状態を想定しながら確認しました。
FF55、IE10は直線になって消えた状態になりましたが、GC61、Opera48ではブロックが壊れた感じになりましたので、skewX(89deg)に変更して公開しています。

N に skewY(90deg) を指定して実験しました。こちらも縦につぶれて直線になりますが、やはり、FF55、IE10は直線になって消えた状態ですが、GC61、Opera48ではブロックが壊れた感じになりましたので、skewY(89deg)に変更して公開しています。

例6へ

サンプル例7の内容

【例7】では、XとYが 45degを非推奨となった O : skew(45deg,45deg) と P : skewX(45deg) skewY(45deg) を実験してみました。想定は斜めの直線で、上記各ブラウザでも斜めの直線になって消えた状態になりました。
横や縦ではブロックが壊れるような感じになっていたGCや(同じwebkit系になった)Operaでも、ブロックが壊れず、直線になって消える状態になっていました。

P : skewX(45deg) skewY(45deg) の方は、なんとなくまだ余裕のありそうな平行四辺形になっていました。

例7へ

参考：skew関連の matrix値を調べてみました

参考情報として以下、GCで、matrix値を調べてみた結果です。
skewX(90deg) = matrix(1, 0, 1.63312e+16, 1, 0, 0)
skewY(90deg) = matrix(1, 1.63312e+16, 0, 1, 0, 0)
skew(90deg) = matrix(1, 0, 1.63312e+16, 1, 0, 0)
skew(45deg,45deg) = matrix(1, 1, 1, 1, 0, 0)
skewX(45deg) skewY(45deg) = matrix(2, 1, 1, 1, 0, 0)
GCのweibkit系でブロックが壊れたようになるのは [1.63312e+16] = [16331200000000000] のような数値が影響していて、よくわかりませんが、FFやIEはなんかうまいことごまかしてやってるのかもしれません。

ということで、FFで、matrix値を調べてみた結果です。
FF / skewX(90deg) = matrix(1, 0, 10000, 1, 0, 0)
IE / skewX(90deg) = matrix(1, 0, -2.28773e+007, 1, 0, 0)
FF / skewY(90deg) = matrix(1, 10000, 0, 1, 0, 0)
IE / skewY(90deg) = matrix(1, -2.28773e+007, 0, 1, 0, 0)
FF / skew(90deg) = matrix(1, 0, 10000, 1, 0, 0)
IE / skew(90deg) = matrix(1, 0, -2.28773e+007, 1, 0, 0)
※skew(45deg,45deg) と skewX(45deg) skewY(45deg)はGCと同じでした。

参考：skewXやYの時の計算はtan(deg)

90deg = 90 * π / 180 = 1.570796325 rad
ということで、 tan(90deg) = の計算結果がブラウザごとに違う、ということかと思われます。

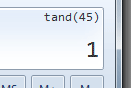
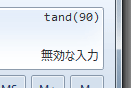
ちなみに、windows付属の電卓の関数電卓機能でチェックしてみると、 tan(45deg)=1 でちゃんと動くのを確認し、tan(90deg)をチェックすると、

「無効な入力」と言われてしまいました。

skewXやskewYを使う時の注意点

90deg , -90deg , 270deg , -270deg は指定しないほうがいい、ということになるかと思います。

※ 2017.10.06 記事改定時に、以前はFFやIE10で実験して書いていた skew(90deg,90deg) については、上記のmatrix値により、GCのwebkit系ではブロックが壊れるので、書くまでもないかと思い、削除しました。
参考までに、
skew(90deg,90deg) = matrix(1, 1.63312e+16, 1.63312e+16, 1, 0, 0)

ちなみに、最近はFFがあまりに重すぎるので、GCをメインブラウザとして、このwebサイトを作ってます。

傾斜変形(シアー)プロパティ

skewX(d)

X軸に沿って角度dで傾斜変形。例 transform:skewX(30deg)

skewY(d)

Y軸に沿って角度dで傾斜変形。例 transform:skewY(30deg)

skew(dx,dy) ※非標準

X軸とY軸に沿ってそれぞれ角度dx,dyで傾斜変形。例 transform:skew(30deg,-30deg)。非標準となったので使用してる場合はskewXやskewYに変更する方が良い。

ページトップへ