2進数の仕様を「考え方を置き換える」ことで応用する
複数の選択状態をたった一つの10進数値で表現することができ、10進数を2進数に変換すると意味が一目で理解できる。
2進数の活用ネタとして、複数の選択状態は10進数1個で表現できる、という内容を紹介します
今回ご紹介するメインのネタは、 『アンケートの複数選択可の項目』の複数選択状態を文字列ではなく、数値で表現する、 というものです。
2進数については一応知ってるけど、自分には関係なーい、なぜならシステムやソフト作ってる人がプログラムで使うものだから、などと思っている人に、web制作者が使えるようなネタを紹介する記事となっています。
対象は進数の活用ネタをまだ知らない、WEB制作営業さんやWEBデザイナーさん、フロントエンド以下略さんを想定しています。
今回の記事は、2進数値は見た目でイメージして別の意味づけをしている、というネタになっています。
このネタで、例えばサーバーのパーミッション設定の644、755などの数値も意味が理解できるようになる、なども最後の方でちょっとだけ紹介しています。
なので、すでに「2進数と複数選択」や「片手で31まで数えられる」「パーミッション設定の数値の意味」について知ってる場合は、
読むまでもない記事かと思います。
2進数はもう一般的だよ~ちゃんと知ってるよ~わざわざ説明すんなよ~などと言われるかもしれませんが、まずは最初に2進数を紹介します
2進数の紹介
簡単に紹介すると「2進数は0と1しか数字を使わない数値」です。
10進数は 0 1 2 3 4 5 6 7 8 9 まで数字を使う数値。
0 1 2 3 4 5 6 7 8 9 までカウントしたら上の桁に1が足され1になり、1桁目が0にもどり、10 11 (中略) 18 19 、上の桁に1が足され2、1桁目は0にもどり、20 21 22 …とカウントする数値…これはいつも普通に使っている数値です。
2進数は 0 1 だけを使う数値なので、0 1 までカウントしたら上の桁(2桁)が1になり、10(いちぜろ) 11(いちいち) その次は上の桁(3桁)が1になり、100(いちぜろぜろ) 101 110 111 、また桁上がりして 1000 1001 … と桁が増えます。十進数なら 999 の次でやっと4桁の 1000 になりますが、2進数では10進数の8 で 4桁の 1000 になります。
10進数で0から16までを5桁の2進数で並べてみます。
00000 00001 00010 00011 00100 00101 00110 00111 01000 01001 01010 01011 01100 01101 01110 01111 10000
2進数を活用する時の重要ポイントなので、知ってると便利なのが 1 が 1個だけの数値です。
00001(2)=1(10) 00010(2)=2(10) 00100(2)=4(10) 01000(2)=8(10) 10000(2)=16(10)
2進数の活用ネタ「片手で31まで数えられる」
テレビドラマ化された小説「すべてがFになる」シリーズのどれかでこのネタを紹介してたような気がしますし、進数関連の記事や先生が持ちネタ的に話すかもしれないので知ってる人もいるかもしれませんが、2進数で『片手で31まで数えられ、両手なら1023までカウントできる』というネタがあります。
右手だけで、小・薬・中・人・親の5桁で、0が指折り状態、1が伸ばした状態で指を曲げ伸ばししながら数えてみてください。
00000-グー、00001-親指、00010-人差し指、00011-人と親、00100-中指、00101-中と親、00110-ピースサイン、00111-フレミングの右手の法則…ここまでで10進数の7、と言う風に指を曲げ伸ばして順に数えてみると、親指だけが1、人差し指だけが2、中指だけが4、薬指だけが8、小指だけが16です。
中指、人差し指、親指の三本の時は7ですが、実はこれは、各指1本だけの数値を足したものになっています。
00111 = 00001 + 00010 + 00100 なので、1 + 2 + 4 = 7 。ということで片手で指が全部立っている状態は 1 + 2 + 4 + 8 + 16 = 31 になり、片手で31まで数えることができるということなのです。
例えば、10011 なら、00001 + 00010 + 10000 = 1 + 2 + 16 = 19で、01010 は 8 + 2 = 10 です。
2進数の基本的な計算(両手で1023までカウントする計算)
2進数の桁を表現する数値(その桁のみ1である2進数)の計算と両手で1023まで数えられる理屈を紹介します。
10進数の各桁だけが1の数字は、1 10 100 1000 10000 … となりますが、これは、10進数の基数が10なので、10の0乗=1、10の1乗=10、10の2乗=100、10の3乗=1000 … のような計算を数学で習ったかと思います。
同様に、2進数の場合は基数が2なので、2の0乗=1、2の1乗=2、2の2乗=4、2の3乗=8…となります。
ということで両手の指を2進数の各桁だとして、それぞれの指が1本だけ立っている状態と階乗計算を並べてみます。
00000 00001 … 1 ← 2の0乗
00000 00010 … 2 ← 2の1乗
00000 00100 … 4 ← 2の2乗
00000 01000 … 8 ← 2の3乗
00000 10000 … 16 ← 2の4乗
00001 00000 … 32 ← 2の5乗
00010 00000 … 64 ← 2の6乗
00100 00000 … 128 ← 2の7乗
01000 00000 … 256 ← 2の8乗
10000 00000 … 512 ← 2の9乗
全部足すと、
11111 11111 … 1023 になり、両手で1023まで数えることができる、ということになります。
2進数の 111 (10進数の7)は旗が3本立っている状態
3桁の2進数と10進数を書いてみます。[000…0] [001…1] [010…2] [011…3] [100…4] [101…5] [110…6] [111…7]
1は絵づらから旗が立っている、などとイメージされたりします。
Cさん、Bさん、Aさんが今事務所にいるかどうかを在席なら1で旗を立てるとイメージして、不在なら0で表現してみます。
| C | B | A | 10進 | 状態 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 全員不在 |
| 0 | 0 | 1 | 1 | A |
| 0 | 1 | 0 | 2 | B |
| 0 | 1 | 1 | 3 | B、A |
| 1 | 0 | 0 | 4 | C |
| 1 | 0 | 1 | 5 | C、A |
| 1 | 1 | 0 | 6 | C、B |
| 1 | 1 | 1 | 7 | 全員在席 |
全員不在 = 000 = 0、A在席 = 001 = 1、B在席 = 010 = 2、C在席 = 100 = 4
[AとB]は 1+2=3、[BとC]は 2+4=6、[全員在席]は 1+2+4=7 となります。
これは3桁の2進数の1と0の状態を[3つの旗]が[立つ=1][立たない=0]と考えて並べてみると[8タイプの結果]となり、それを10進数の0から7で表現できることを意味します。
例では、3桁の2進数 → 3本の旗 → 在席・不在のマークと表現しています。
表組左の0と1を眺めるだけで、ABCの在席・不在が一目で判別でき、さらに10進数の1つの数値で表すことができました。
アンケート集計に使ってみるなどの応用が考えられます
「在席・不在」を「選択・非選択」とするとアンケートの複数選択可の選択状態を10進数1個で表現するアイデアになります。
2進数3桁の旗を選択肢と考えると、全部旗が立っている状態(10進数の7)は3つが選択されていると表現できます。
アンケートのあなたの趣味は何ですか?(複数選択可)などで、項目が3つあった場合、全部選択されてる場合は [7] 、項目が10個で全選択なら [1023]という数値になります。
アンケート内容をエクセルなどでリスト化する時に
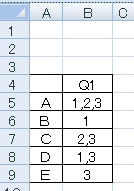
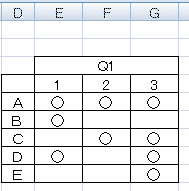
などとセルにカンマ区切りで選択された数字を並べたり、選択状態をそのまま表にするのではなく…
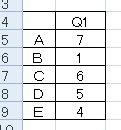 のように数値一つで表現できるので、
のように数値一つで表現できるので、
エクセルで集計やグラフ化、並び替えは1個の10進数で作業できるようになります。
[選択項目 3]だけ選択している人を抽出する場合、値が4(100)のデータを集めます。[選択項目 1と2]を選択している人なら、3(011)、[選択項目 1と2と3]を選択している人なら、7(111)です。
(蛇足的ですが)ここで、じゃあ、1だけと1と2、1と3、1と2と3のように、1を含むパターン全部はどうやって集めるんだ!?と実践的に考える人がいるかもしれません。
プログラムではビット演算(次の記事で紹介)を使いますが、エクセルの普通の関数ではビット演算はできないようなので、単純にエクセルで集計する時は、選択肢1は1桁目が1である数、2進数の001、011、101、111なので、10進数値の 1と3と5と7 を集めるという方法になるかと思います。
途中まとめ
『複数の項目を選択している状態を1個の10進数で表現できる』逆に言えば、『10進数を2進数に変換すると、旗が桁の位置に立っているイメージ図になる』
というように、数値に意味を付加するという考え方を知っているだけで、プログラマ以外でも使える、何かアイデアの素になるかもしれない、などと思ったりします。
検索してたら見つけた類似内容の質問
参考:checkboxで取得した複数の値を、一つのフィールドに保存する方法を教... - Yahoo!知恵袋
という数年前の質問とその回答がありました。
質問:「映画」「音楽」「釣り」「パソコン」「車」の項目のcheckbox取得結果を データベースに入れたい。1つのフィールド(※DBの保存場所のようなもの)に値を入れるにはどうすればいいか?
で、回答がカンマ区切りで文字列で入れればいい。というものになってました。ということは、
Aさん:映画,釣り
Bさん:映画,音楽,釣り,パソコン,車
Cさん:音楽,パソコン
というようなデータをデータベースに入れることになります。
データベースから集計する時はデータの文字列から正規表現などで抽出するような感じで回答している様子です。
回答している皆さんの中には、ホントはビット演算でやれば簡単、という知識があったりする人がいるはずだと思うのですが、長年プログラマやってる人でも、自力で本読みからのプログラム作成練習で習得していった人は、案外基本知識としての進数や論理演算関連は使わなくても仕事ができるので、文字列でデータを入れる方法しか知らない人がいるのかもしれない、などと思ったりもします。
また、よく分かっていない人に質問サイトの回答欄のようなところで、無料で飯のタネを教えるような気がなかったりするのかもしれず、素人っぽくてもとりあえず人に聞かずにある程度のものが作れるようになったら、もっと楽にやる方法は自分でweb検索すればいろいろ記事書いている人がいるので、yahoo知恵袋のような、本来は意見交換のコミュニケーションをするために質問するのが本質の場所で聞かなくても、理解して使えるようになる、などと思ったからなのか
「カンマ区切りの文字列入れればいいんじゃない?」という適当な回答しかないのかもしれない、と思ったりもしました。
これはこれで、正規表現やカンマ区切りで文字列分割などの勉強になるし、実際にやろうとしていることは普通にできるので、正解不正解はないのですが、質問者が「ビット演算?」などと質問しているけれど、回答している皆さんがスルーしている点について、今回のネタと同じ話なので、以降でその方法を紹介してみます。
今回のテーマ(2進数でイメージすると複数選択状態を1つの10進数で表現できる)がそのまま使える
「1:映画」「2:音楽」「3:釣り」「4:パソコン」「5:車」とした選択肢を以下のように並べてみます。
54321 ←選択肢の番号(逆に並べてる)
00000 …0
00001 …1
00010 …2
00011 …3
00100 …4
…中略…
11111 …31
先ほどと同様、直感的に文字の並びを見るだけで、二進数の桁が選択状態を表現していて、10進数に変換すれば数値化可能、と簡単に説明できるかと思います。
Aさん:00101…5 ←1:映画,3:釣り
Bさん:11111…31 ←1:映画,2:音楽,3:釣り,4:パソコン,5:車
Cさん:01010…10 ←2:音楽,4:パソコン
なので、この場合、右にある10進数の値をデータベースの1つのフィールドに入れる、ということになります。
Aさん:5 / Bさん:31 / Cさん:10
質問者が「1:映画=1」「2:音楽=2」「3:釣り=4」「4:パソコン=8」「5:車=16」と書いていますが、実は回答者よりも質問者の方が進数活用の話では正解に近い印象でした。
それぞれのみを選択している状態を並べてみると、
00001 …1(10進数) → 1:映画=1
00010 …2(10進数) → 2:音楽=2
00100 …4(10進数) → 3:釣り=4
01000 …8(10進数) → 4:パソコン=8
10000 …16(10進数) → 5:車=16
となり、複数選択状態の数値は、2進数に変換した時に1が一つしかない数値(次回記事でこの「ビットマスク」を活用して個別の選択を抽出する方法を紹介してます)の足し算、というものを使って、
Aさんの映画と釣りなら、1+4=5
Bさんの映画・音楽・釣り・パソコン・車は1+2+4+8+16=31
と計算した値をデータベースに入れると文字列でやるよりもデータ量が少なくなり、単純になります。
数学っぽく計算式を書くと、[1:映画は 2^0(2の0乗) = 1] [2:音楽は 2^1(2の1乗) = 2] [3:釣りは 2^2(2の2乗) = 4] [4:パソコンは 2^3(2の3乗) = 8] [5:車は 2^4(2の4乗) = 16] です。
ちなみに、複数選択状態を計算する時に「足し算する」というのが分かりやすくなるためのイメージを一応書いておきます。
例:1と2と5を選択の時は?選択場所の旗で、10011 です。
桁が1だけの数値を縦に並べると…
10000 (10進数では16) +
00010 (10進数では2) +
00001 (10進数では1)
で
10011(つまり16+2+1)
10011(10進数では19)
パーミッション設定の話も同じ考え方です
フロントエンドエンジニアさんがサーバにFTPでファイルをアップロードする時に出てくる用語であるパーミッション設定について、もしかすると知らない人がいるかもしれませんので、簡単に今回の記事の内容との関連について少し紹介しておきます。
パーミッション設定値が 777 は、
「7(8進数) = 111(2進数)」が3つ並んでいることを表現しています。
つまり、777 = [111][111][111] で、1である状態が3つずつ、合計9つ設定されています。
644は、[110][100][100] です。
なので、パーミッション設定は、全部で9つの項目が1か0に指定されているものになります。
UNIX系OSで動いてるサーバにFTP等でアクセスしたときのファイル操作の権限等を設定する項目で、特にフロントエンド以下略さんが実際に遭遇する可能性がある事例としては、お客さんのweb更新作業時に、サーバ上からファイルやフォルダを削除しようとするとできない場合があったりするような件です。
分からなければ、サーバ会社に丸投げで削除依頼すればいいんですけど、もしかすると昔アップロードした人が、ファイルの権限を変更して削除できないようにしているだけだったりして、FTPソフト上で設定を変更するだけで簡単に削除出来たりする場合もあったりなかったりします。
で、パーミッション設定の例えば 644 は、最初の[6]がオーナーのアクセス権限、次の[4]がグループメンバーの権限、最後の[4]がその他の利用者の権限を指定しています。
これまでのように2進数の旗立てで権限を表現すれば、サーバのファイルやフォルダは
オーナー、グループメンバー、その他利用者ごとに3つの機能、
[r:ファイルを読める][w:ファイルを上書き・削除可][x:プログラムを動かせる]を設定することができます。
[O:オーナー][G:グループメンバー][U:その他利用者]と上記のrwxの記号で表組にしてみます。
| O | G | U | ||||||
| r | w | x | r | w | x | r | w | x |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 6 | 4 | 4 | ||||||
オーナーには[r]と[w]を許可し、グループメンバーとその他利用者には[r]のみ許可する、というのを 644 という数値で設定しています。
パーミッション設定で検索した時に説明サイトがいろいろ出てきますが、大抵、r=4,w=2,x=1と省略して書いてますので単純にそういう数値として覚えているだけの人がいるかもしれませんが、その数値は2進数の桁とフラグ立てを権限許可に見立てて表現しているということなのです。
3つの機能への許可設定を2進数で表現し、それを8進数に変換すると、rは4、wは2、xは1になり、全部足すと最大で7、という値になる、ということなのです。
※ちなみに、最大7なので、10進数でも8進数でも変換すれば同じ数値ですが、パーミッションについては8進数が使われます。
ということで、複数の選択状態を一つの10進数数値で表現するために2進数を活用する、というネタを紹介してみました。
今回記事を読んだ人は、何度も書いておきましたので、サブリミナル効果的に、7=111 が脳にこびりついてしまったのではないかと思ったりします。
ついでにアイデアのタネとして覚えておくなら、10本指の各指一本の、512 256 128 64 32 16 8 4 2 1 の足し算で 1023までの数値が表現できるというネタかと思います。
一度、指を曲げ伸ばして、1023まで数えてみるのも、しんどいけど面白いかもしれません。原森は64当りで断念しましたが…。
2進数はプログラムの基本中の基本なので、知っておくとこれからプログラム的なことをやろうとした時に自動的に脳内に情報が発火してきて楽な感じで書くことができるアイデアを思いつくことがあるかもしれません。
「っていうか、10進数にした値から個別に選択しているのを取り出す時はどうするんだ?」
と、ここで今回のネタ知識を知ったばかりの人は、思ってしまうかもしれません。
選択されてるかどうかを調べる方法はビット演算を使って調べることになります…が、
それについては次の記事で紹介したいと思います。
興味があれば、続けて次の記事をフッターの[NEXT]リンクなどから閲覧してみてください。
とりあえず、お疲れさまでした。